A short history of "Liesegang rings"
The periodic precipitation process known as "Liesegang phenomenon" has now been investigated for more than 100 years. Although during the 20th century the phenomenon caught the imagination of thousands of scientists from different fields, and hundreds of papers have been published on this topic formation of Liesegang patterns still lacks of any complete mathematical description.

Patterns in nature
In the last decades of the 20th century different kinds of chemical, physical and biological pattern formations have excited an ever increasing interest in the scientific community. In chemical patterning one of the most intensively investigated area was the so-called Belousov-Zhabotinsky reaction, but there were many publications about viscous fingering, diffusion limited aggregation, morphogenesis of fungal colonies and some other simple living bodies, and last but not least patterning during electrochemical deposition too.
Although at first sight the above mentioned systems are quite different there are many similarities in the way they form the corresponding patterns, and the methods by that they can be handled. All of them contain at least one or several diffusion-limited steps, while the formation of the spatial or spatiotemporal order is always a result of a complicated interplay of these and the underlying chemical, physical or biological processes.

Mathematics and the modeling of reaction-diffusion processes
Mathematical description of such systems consists of so-called reaction-diffusion differential equations. Unfortunately these are usually systems of coupled nonlinear partial differential equations, that cannot be treated by standard analytical methods. The only viable way is the application of different numerical methods. Numerical solution of such systems of equations is computationally very demanding, moreover it is sometimes computationally prohibitive even nowadays.
The story of the so-called Liesegang phenomenon is good example for this problem.

Typical Liesegang patterns: silver-chromate rings formed in a gelatine layer and two slightly anomalous linear systems

Liesegang patterns
Liesegang patterning is a special type of chemical pattern formation in which the spatial order is formed by density fluctuations of a weakly soluble salt. From analytical chemistry we know many different reactants that form a precipitate (sparingly soluble salt) when they react with each other. A good example for this behavior is the reaction of silver-nitrate (AgNO3) and potassium-dichromate (K2Cr2O7).
If one of these components is evenly distributed in a swollen gel (e.g. in gelatine), and the solution of the other diffuses into it, the spatial distribution of the slowly forming precipitate will not be continuous. A series of precipitate zones (bands or rings depending on the geometry of the experimental setup) will form according to some simple scaling laws.
The figure above shows a one and a two dimensional Liesegang pattern.

Raphael Eduard Liesegang and the first scientific paper about periodic precipitation published in 1896

Beginning of the history of periodic precipitation
Such kind of chemical patterning was first mentioned in 1855 by Frederic Ferdinand Runge. As a reaction medium he has used simple filter-paper wet by an electrolyte solution. He called his patterns "self-painting pictures", and published a whole book about them. Nowadays we use the term "self-organisation" for general designation of such phenomena, and probably thousands of articles can be found in the literature about it.
But Runge's discovery was unfortunately too early. Nobody respected his work, and precipitate patterns have fallen into oblivion until 1896. In that year Raphael Eduard Liesegang a German photographer and chemist was experimenting with gelatine layers swollen by solution of potassium-dichromate. He accidentally dropped a small crystal of silver-nitrate onto a specimen, and was astonished that the precipitate formed concentric rings about it. Distances between adjacent rings were always increasing outward, and it was possible to reproduce the phenomenon with a one dimensional arrangement in a test tube too.
Later Liesegang has systematically investigated this phenomenon and published many papers about his findings. As his work was the first detailed investigation on the field of spatiotemporal precipitate patterns, "quasiperiodic precipitation" was called Liesegang phenomenon by the posterity. (It is usual to talk about Liesegang rings or Liesegang bands too.)

Left: Wilhelm Ostwald who has suggested the first quantitative theory
(supersaturation model) for periodic precipitation and has given
it the name that we use today: "Liesegang phenomenon".
Right: Title page of
the book in that Ostwald described the mentioned model.
The first model
Liesegang has shown his results to Wilhelm Ostwald, who has published the first possible explanation of quasiperiodic precipitation in his book about general chemistry in 1897. This is the so-called supersaturation theory, that later appeared in many publications during the 20th century. In the first decades almost all of the papers concerning this subject were about different experimental findings. In 1923 Jablczinsky has noticed that distances of Liesegang rings measured from the origin of the pattern are always members of a geometrical series. This is the most basic scaling law, the so-called spacing law of Liesegang patterning.
In these years Liesegang patterning was discovered in many different systems, but at the same time many different anomalies has been reported too.

Development in the 20th century
Although many qualitative explanations different from Ostwald's model were suggested in the first decades, only few of the scientists tried to develop a mathematically exact description, and even these trials were essentially unsuccessful. This is certainly not surprising taking into account the formerly mentioned ill-conditioned nature of the reaction-diffusion equations.
In the second half of the 20th century there were some significant changes both on the experimental and theoretical fields.
Experimental methods became more sophisticated and their results more accurate and detailed. Papers published for example by John Ross, Soichi Kai and Stefan C. Müller contained especially in-depth investigations, but these are only a few of the several thousand articles published since 1896. (In 1952 Kurt H. Stern mentioned more that 600 papers in his review article.)

The advent of high speed computers
In the 90-es the power of low end or normal desktop computers became close to the level that is adequate for numerical treatment of problems like solution of reaction-diffusion differential equations. This opened a new age in history of the Liesegang phenomenon. The first really thorough numerical study was performed by Polezhaev and Müller, using their own model, that was essentially an extension of the supersaturation theory, suggested in 1897 by Wilhelm Ostwald.
This model was later extended and investigated by Krug et al. Chopard et al. has developed a lattice-gas model for simulation of 2D Liesegang patterns. Later the same system was used by Antal et al. for numerical investigation of the so-called spinodal decomposition scenario.
Despite these efforts, no general model of Liesegang patterning has been proposed till now. Although from experimental point of view it is a rather well known phenomenon, there were many effects and anomalies without even qualitative explanation.
Until 2003 no models have ever addressed the problem of revert patterning, formation of helices, ball-like or meniscus shaped zones, propagating defects observed in many of the patterns, or the so-called double banding effect (two patterns in the same system with different frequencies).

The IDNB model
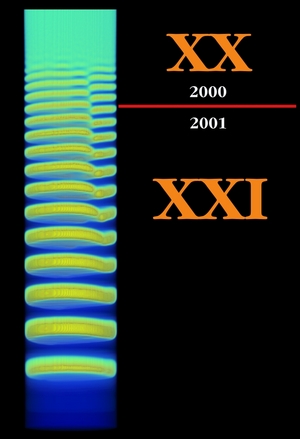
The figure on left shows an early result of the IDNB model. From historical point of view this is a noteworthy picture, beacuse this simulation has been started on new year's eve of 2000 on a four-processor cluster (and then I went to drink some champagne with my friends). This means that about the first three precipitate zones were computed in the 20th century, while the subsequent ones belong to the 21st century history of Liesegang patterning.
At that time I still did not understand many aspects of the phenomenon. For example my model was able to reproduce certain stochastic effects and even the cause of revert patterning was clear. At the same time I had only dim ideas about the formation of helical patterns.
The final form of the IDNB model got ready only in 2003 while I was walking on the bank of river Tisza.